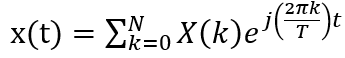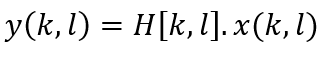(suite de l’article précédent)
Merci à Christophe BAILLOT, enseignant Télécom à l’IUT R&T du Pays de l’ADOUR pour sa relecture et ses commentaires.
III) L’orthogonalité : la base de la transmission
Principe fondamental : Bande de base/transmission autour d’une porteuse
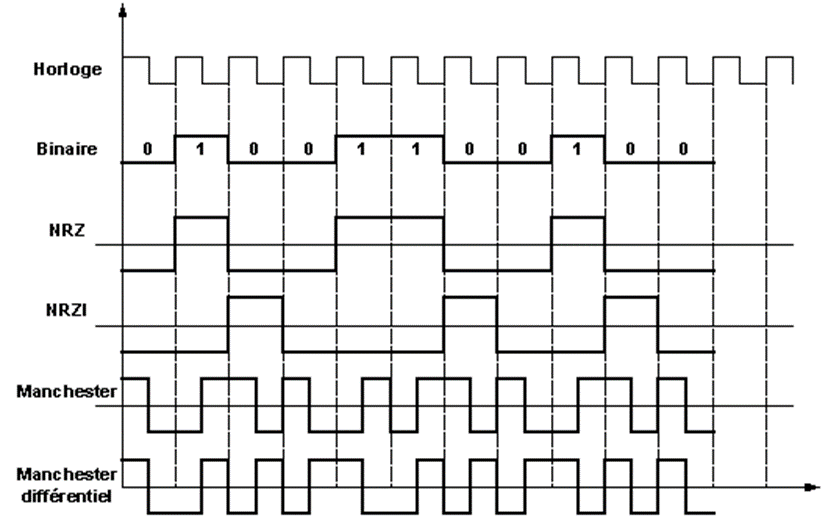
Lorsqu’on souhaite transmettre une information binaire, on utilise un code en ligne pour transmettre la valeur du bit en bande de base. Ce code peut éventuellement transmettre l’horloge d’émission. Les types de codes classiques sont les codes RZ, NRZ, Manchester, Miller qui sont des codes antipodaux.
Figure 8 : Codes en ligne
La figure précédente représente des codes en ligne pour la transmission en bande de base.
Si l’on souhaite transmettre le signal autour d’une fréquence porteuse, le signal binaire est le modulant car il vient moduler la porteuse. Le récepteur démodule le signal autour de la fréquence porteuse.
Le signal binaire est un signal orthogonal, puisque le produit scalaire des deux informations binaires sur la durée du bit est nul.
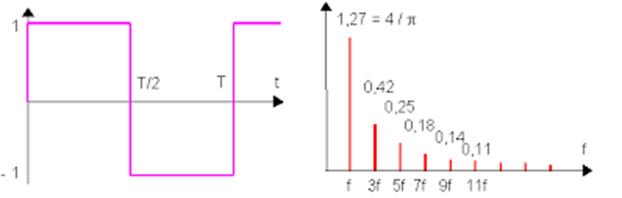
Si l’on prend un signal carré, périodique (par exemple le signal d’horloge) alors le spectre du signal binaire, c’est-à-dire la distribution de la puissance sur les harmoniques, est théoriquement infinie.
Figure 9 : Signal carré et sa transformée de Fourier
Sur la figure 9, le signal est un signal carré périodique.
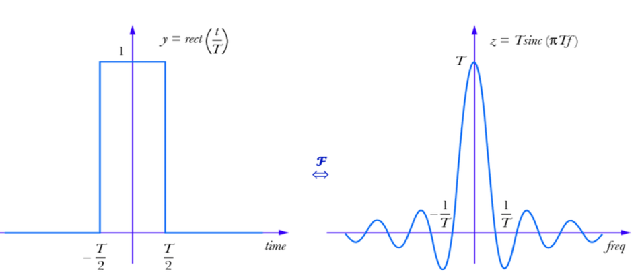
Transmettre une information binaire consiste à émettre un signal rectangulaire, appelé signal porte :
Figure 10 : Représentation du signal porte et de sa transformée de Fourier
La transformée de Fourier d’un signal porte est un sinus cardinal, dont le lobe principal à pour largeur de bande B=2/T. On retrouve donc le principe évoqué précédemment, plus le débit est rapide, plus la durée du signal porte est courte et plus la bande est importante.
Par exemple :
- Pour un débit de 1000 bits par secondes, la durée de la porte est de 1 ms.
- Pour un débit de 1 Mbits par seconde, la durée de la porte est de 1 µs.
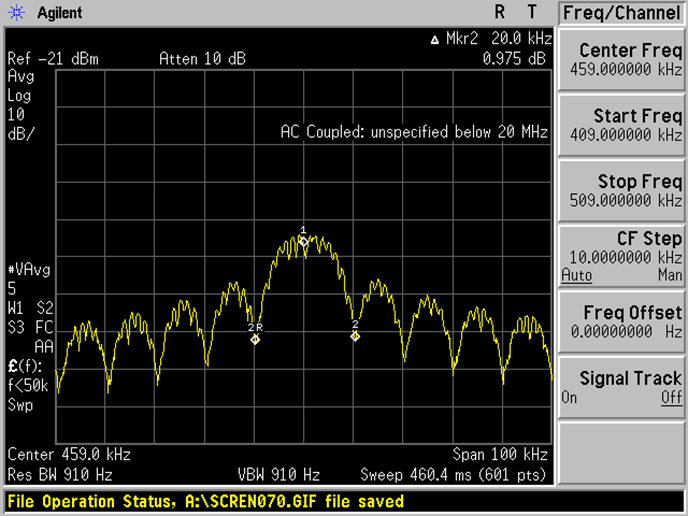
Dans le cas d’une transmission d’information, le signal binaire est une séquence binaire aléatoire (0100111101101). Le spectre en dB à la forme suivante :
Figure 11 : Le spectre d’un signal QPSK
Le signal apporte de la puissance sur les bandes voisines, on parle d’interférence. Pour limiter cette interférence, la solution consiste à filtrer le signal.
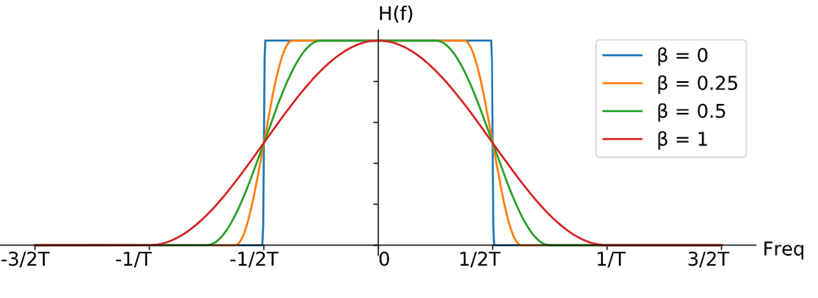
Par exemple, voici la fonction de transfert d’un filtre passe-bas appelé filtre en cosinus surélevé (figure 12).
La fonction de transfert en bleu est sélective. Sur la figure 4 cela reviendrait à ne conserver que le demi-lobe principal : on multiplie le spectre du signal par la fonction de transfert du filtre : Y(f)=H(f).X(f), X(f) est le spectre de la figure 4 et H(f) la fonction de transfert de la figure 5.
Figure 12 : Fonction de transfert du filtre en cosinus surélevé
Toutefois, le fait de filtrer déforme le signal dans le domaine temporel. Comme on souhaite conserver la condition d’orthogonalité dans le domaine temporel, on utilise un filtre de Nyquist. Cela va éviter l’interférence en temps, nommée interférence inter-symbole ou IES ou IIS : l’échantillon à la période T en sortie du filtre n’est pas interféré par les bits filtrés et émis précédemment.
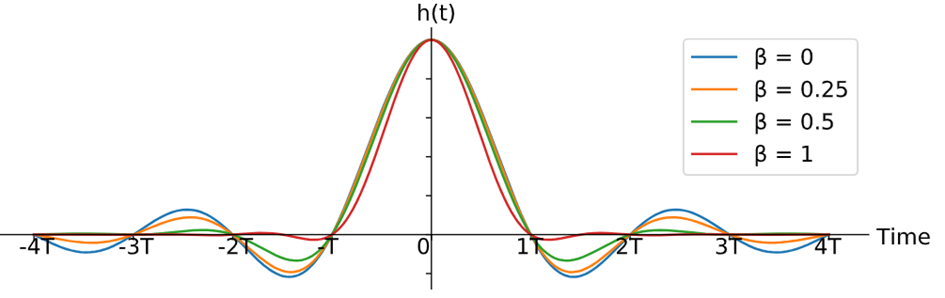
On s’aperçoit sur la figure 13 que la forme temporelle d’un signal porte après filtrage de Nyquist s’étale dans le temps mais aux instants kT, k entier, l’amplitude du signal filtrée est nulle. Sur la figure 13, on modifie la valeur du roll-off (sélectivité du filtre)
Figure 13 : La représentation du signal de la porte après filtrage
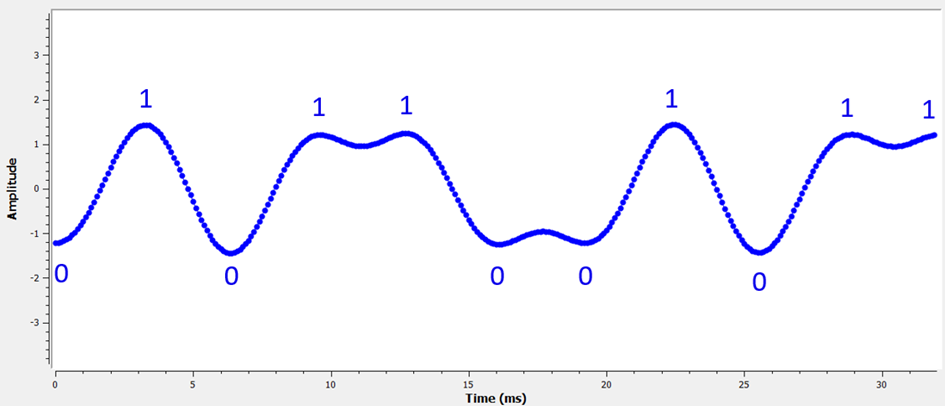
Ainsi, l’application du filtre sur la séquence binaire suivante 01011001011 donne le signal temporel représenté sur la figure 14 (il s’agit de la convolution du signal précédent aux instants d’échantillonnage de la séquence binaire +1/-1):
Figure 14 : La représentation d’une séquence binaire filtrée
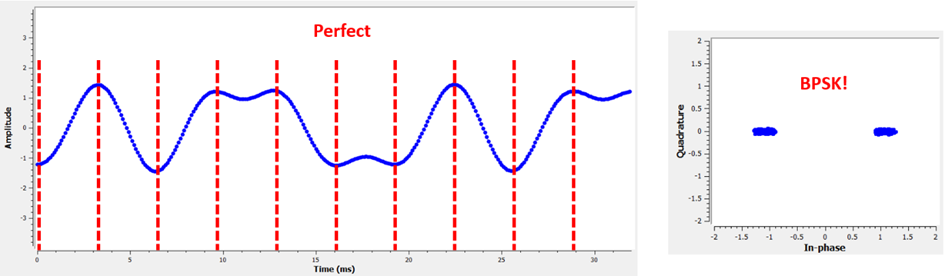
L’orthogonalité permet de préserver qu’au moment de l’échantillonnage, la valeur de l’amplitude est +1 ou -1
Figure 15 : L’orthogonalité dans le domaine temporel
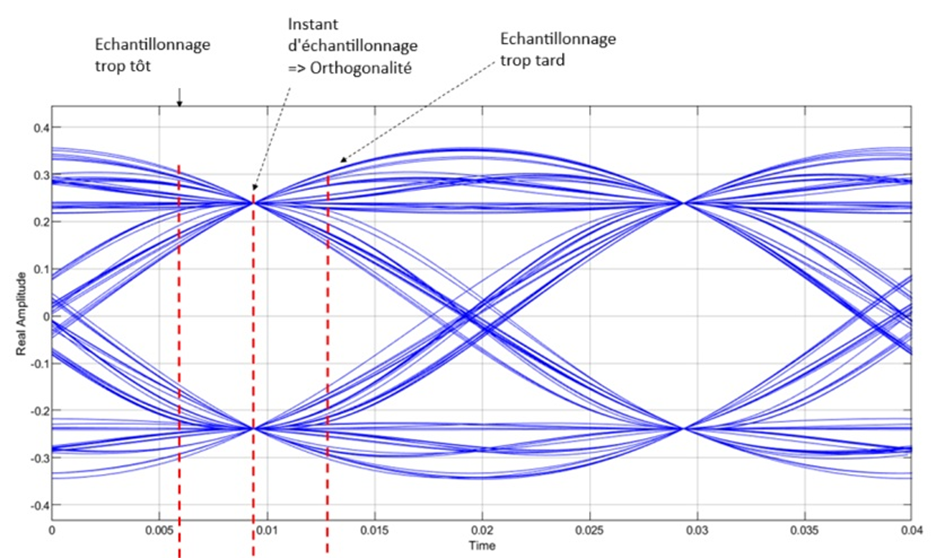
En général, on représente la forme temporelle par le diagramme de l’œil. Cela consiste à superposer 3 bits sur une figure. Pour comprendre facilement, supposez prendre en photo les 3 premiers bits, puis prendre en photo du bit 2 au bit 5 et vous superposez (calque) les deux photos et continuez ainsi. On obtient ainsi la figure 16 dite diagramme de l’œil montrant l’orthogonalité du signal filtré.
Figure 16 : L’orthogonalité dans le domaine temporel – Diagramme de l’oeil
Pour les réseaux mobiles 3G, le spectre opérateur est de 5 MHz. Il s’agit de l’occupation spectral d’un chip à 3,84 Mbps par un filtre en cosinus surélevé de coefficient 0,22. La bande occupée est donc de 3,84*1,22= 4,69 MHz.
Le signal reçu est donc déformé : Le retard apporte de l’interférence inter-symbole qu’il est nécessaire de compenser. En réception, un égaliseur a pour rôle de s’affranchir des perturbations du canal. En 3G, on utilise un récepteur rake pour contrer les phénomènes de multi-trajets. Afin que plusieurs utilisateurs puissent émettre dans la même bande radio, la 3G s’appuie de plus sur un multiplexage par code Orthogonal (Direct Spread Code Division Multiple Access). Les codes orthogonaux sont générés par des séquences de Walsh Hadamard. Ce sont des séquences orthogonales à condition d’être synchronisées. La synchronisation est réalisée par des codes de Gold en 3G, qui ont de bonnes propriétés d’intercorrélation et d’autocorrélation.
La 3G utilise donc, dans le domaine temporel, un vecteur d’étalement orthogonal nommé OSVF (Orthogonal Spreading Variable Factor) en plus du filtrage par un filtre de Nyquist.
L’un des soucis de la 3G est la complexité du récepteur rake, le signal étant déformé sur une large bande, la 4G propose d’utiliser un découpage en fréquence et non plus en temps appelé modulation OFDM.
L’OFDM divise le canal de transmission en plusieurs sous-porteuses orthogonales, permettant la transmission parallèle de données sur différentes fréquences. Le principal avantage est la simplicité d’implémentation avec la FFT/IFFT.
L’orthogonalité se calcule cette fois-ci sur les sous-porteuses : soit deux sous porteuses v1(t) et v2(t), le produit scalaire est calculé par l’intégrale du produit des porteuses sur la durée d’un symbole. L’intégrale est nulle si la durée d’un symbole est inversement proportionnelle à l’espacement entre sous porteuses. En 4G et 5G, la durée d’un symbole est donc l’inverse de l’écart entre fréquence (SCS ; SubCarrier Spacing).
La Transformée de Fourier, en réception, revient à un produit scalaire entre le signal reçu y(t) et l’exponentielle à la fréquence fp. Cela représente donc la quantité de signal reçu dans la fréquence porteuse.
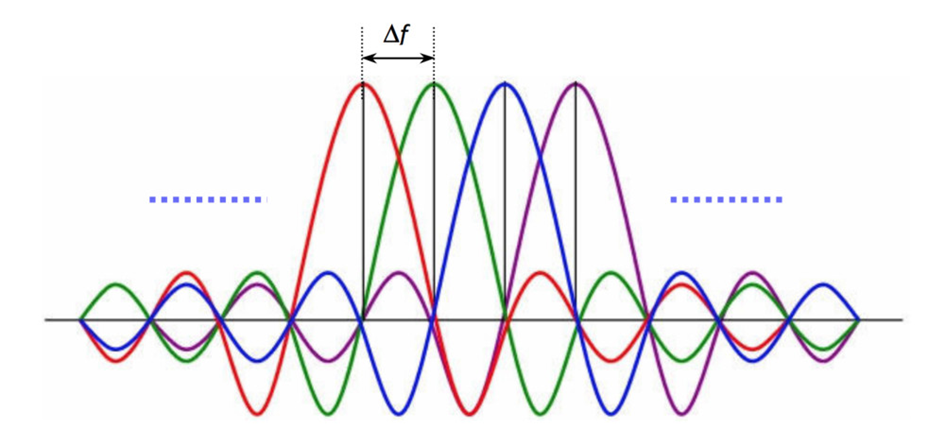
Ainsi, de manière similaire aux figures 15/16, on peut représenter l’orthogonalité dans le domaine fréquentiel par la figure 17.
Figure 17 : L’orthogonalité dans le domaine fréquentiel
L’axe des abscisses est en noir. On remarque que l’amplitude des ondes est soit maximale soit nulle à la fréquence de réception, ce qui prouve l’orthogonalité en fréquence.
Malgré ses avantages, l’OFDM présente certaines limitations :
- Sensibilité à l’effet Doppler
- Perte d’orthogonalité en cas de décalage fréquentiel
- Performance limitée dans les canaux à forte mobilité
- Nécessité d’un préfixe cyclique réduisant l’efficacité spectrale
En effet, l’OFDM a pour objectif de moduler différentes sous porteuses espacées par un écart en fréquence SCS (15 kHz en 4G).
En reprenant la figure 17, le signal qui est transmis est une modulation de chaque sous porteuse :
avec X(k) le symbole qui est transmis sur la k-ième sous porteuse. Cette représentation n’est rien d’autre que la transformée de Fourier inverse et par conséquent la transformée de Fourier est vue comme un filtre adaptatif qui pourra reconstruite les symbole X(k).
Le synoptique a fait l’objet de quelques articles dont celui du 13 septembre 2013 (article OFDM)
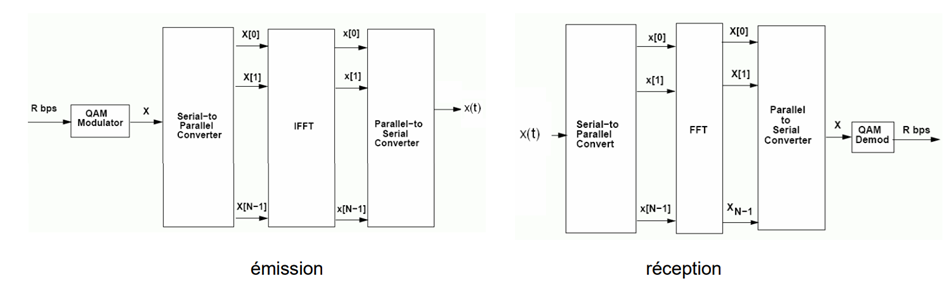 Figure 18 : Synoptique émission/réception OFDM [3]
Figure 18 : Synoptique émission/réception OFDM [3]
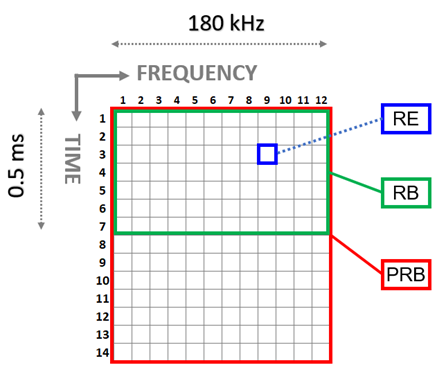
On définit en 4G un bloc de ressource qui représente le symbole OFDM à transmettre. Le bloc de ressource à une composante en temps et en fréquence :
Ainsi, le signal reçu aura une caractéristique dans le domaine temporel n et fréquentiel m :
Avec k l’indice du symbole, l l’indice de la sous-porteuse, H le canal de propagation.
La technique d’égalisation a pour objectif de calculer l’inverse de H afin d’estimer au mieux le signal émis à partir de la séquence reçue . Pour mesurer la distorsion du canal en temps et en fréquence, on insère des signaux de références. Il s’agit de séquence d’apprentissage, le récepteur sait ce qu’il doit recevoir et compare le signal reçu de la séquence d’apprentissage qu’il aurait du recevoir. Cette déformation permet d’estimer le canal au prix d’une estimation répétitive en temps et en fréquence.
En 4G, le signaux de références sont distribués sur toute la bande en fréquence et sur le temps.
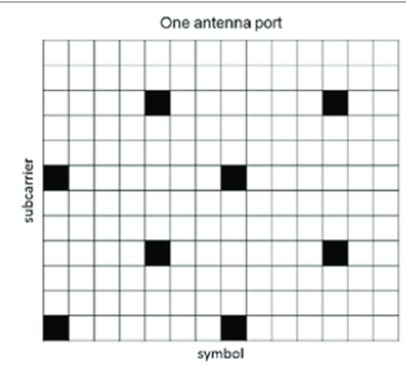 Figure 19 : Séquence d’apprentissage en 4G
Figure 19 : Séquence d’apprentissage en 4G
Le canal de propagation est donc estimé dans le domaine temporel et fréquentiel. Les échos vont apporter un délai dans la réception, la vitesse va apporter un décalage en fréquence.
On va représenter l’estimation du canal de propagation en temps et en fréquence mais il serait plus efficace d’estimer les retards et le décalage (figure 19 [5])
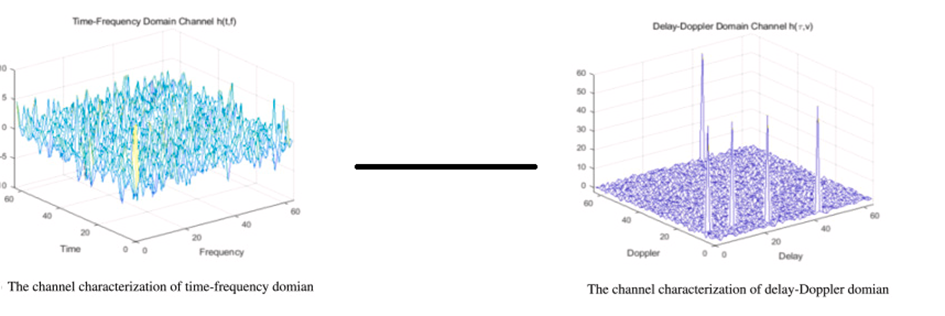 Figure 20 : Représentation temps/fréquence et délai/doppler
Figure 20 : Représentation temps/fréquence et délai/doppler
Le principe de l’OTFS est de calculer le canal de propagation dans sa dimension délai/doppler.
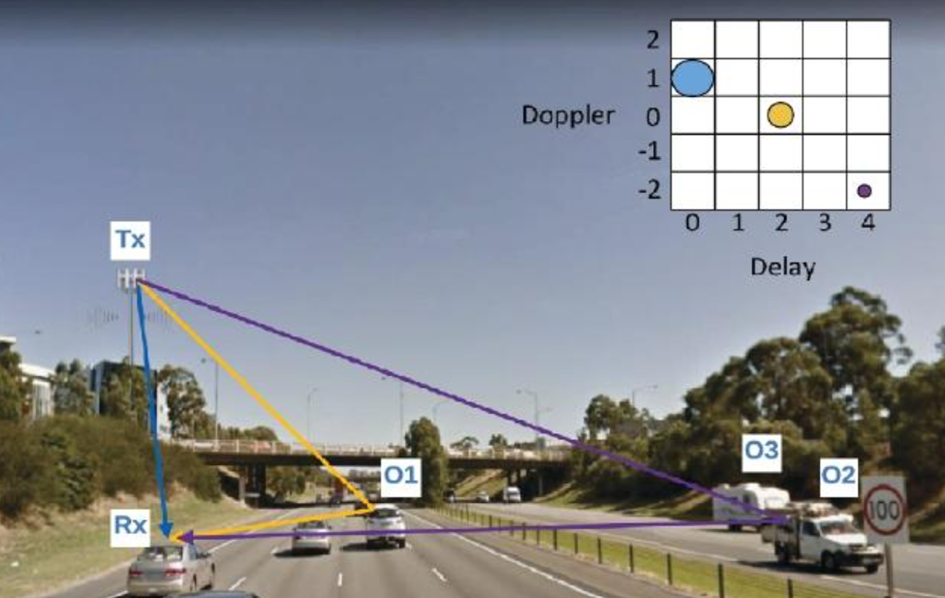
[5] propose une figure illustrative (figure 21): Le véhicule RX s’approche de la station de base, le signal direct est affecté d’un Doppler qui est calculé à partir de la vitesse du véhicule. Le même signal est réfléchi par le véhicule O1 qui roule devant lui à la même vitesse. On constate donc un délai dans la réception mais pas de Doppler, contrairement au véhicule 02 qui roule dans l’autre direction pour lequel le Doppler est important sur le retard de réception.
Figure 21 : Représentation du délai et du Doppler (Figure extraite du [5])