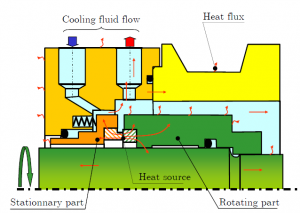
Analytical model for full film lubrication
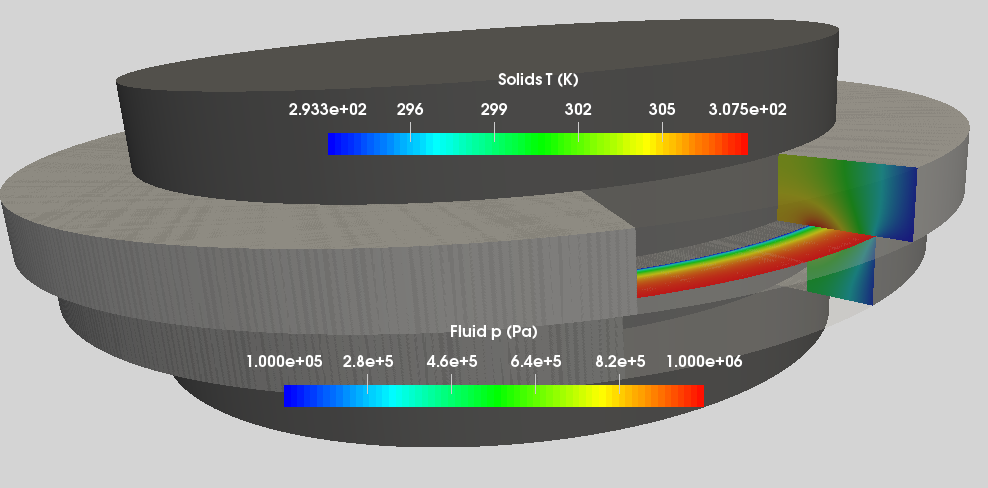
In this post, a first model for full film lubrication is proposed. It will allow to determine the seal faces temperature, the thickness of the film between the faces, the friction torque, etc.
If the distance between the faces is assumed to be equal to the mean film thickness, the dissipated power by viscous friction is:
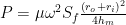
This power is transferred to the seal rings by conduction. According to post# 1, we have:
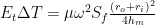
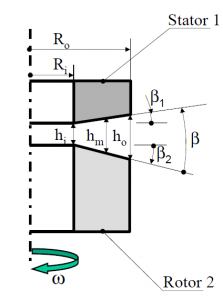
According to post# 3, the film thickness is given by:
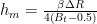
The coning angle 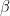 is due to the faces deformations as explained in post #2:
is due to the faces deformations as explained in post #2:

Finally, the fluid viscosity 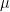 is a function of the local temperature. By using an exponential law, we have:
is a function of the local temperature. By using an exponential law, we have:
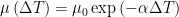
where 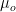 is the viscosity at the reference temperature and
is the viscosity at the reference temperature and 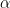 the thermoviscosity coefficient.
the thermoviscosity coefficient.
A non linear equation of the seal faces temperature is obtained:

It is convenient to use a dimensionless form of this equation. For that a temperature scale based on the thermoviscosity coefficient is used:
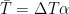
Then the previous non linear equation temperature becomes:

In this equation 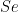 is the sealing number and is a kind of thermal loading number of the seal face:
is the sealing number and is a kind of thermal loading number of the seal face:

The second dimensionless number, 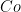 , is the coning number. It represents an initial coning of the faces due to mechanical loading (fluid pressure) or wear of the faces:
, is the coning number. It represents an initial coning of the faces due to mechanical loading (fluid pressure) or wear of the faces:

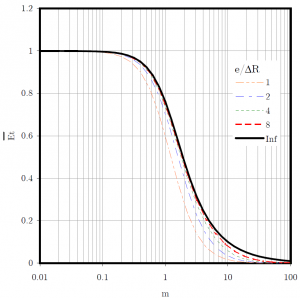
According to governing equation, the seal faces temperature rises with the sealing number, 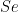 . However, the magnitude of this temperature is reduced by the decrease in viscosity with temperature (exponential term) and the increase in film thickness with temperature (denominator). A positive initial coning number,
. However, the magnitude of this temperature is reduced by the decrease in viscosity with temperature (exponential term) and the increase in film thickness with temperature (denominator). A positive initial coning number,  , will increase the film thickness and thus reduce temperature whereas a negative value will produce the invert.
, will increase the film thickness and thus reduce temperature whereas a negative value will produce the invert.
The governing equation can be easily solved by using Excel for example. When the temperature of the faces is known, it is then possible to compute the film thickness, the leakage flow, the friction torque, etc. The next figure presents the dimensionless temperature rise as a function of the sealing number for different values of the coning number.
 In the case of negative coning number, the temperature can not be lower than
In the case of negative coning number, the temperature can not be lower than  to avoid negative coning and film thickness. This situation is not realistic and will lead to faces contact. To analyze
to avoid negative coning and film thickness. This situation is not realistic and will lead to faces contact. To analyze
this effect, the minimum film thickness can be expressed in a dimensionless form:

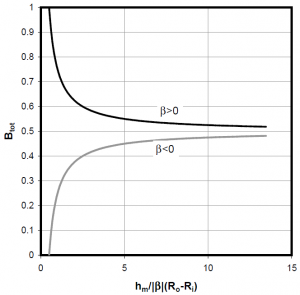
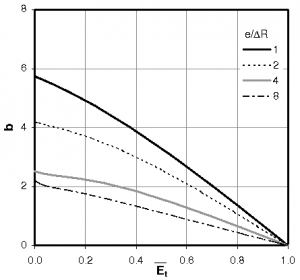
 The film film thickness is presented as a function of the sealing number;
The film film thickness is presented as a function of the sealing number; 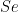 , for different values of the coning number
, for different values of the coning number 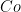 in the next figure. As expected the film thickness is an increasing function of
in the next figure. As expected the film thickness is an increasing function of 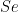 . For positive coning number, the minimum film thickness can not decrease below a threshold avoiding faces contact. For negative or null values of
. For positive coning number, the minimum film thickness can not decrease below a threshold avoiding faces contact. For negative or null values of 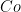 , the film thickness can reach zero at low sealing number values. In this case face contact will be experienced. According to my experience, the dimensionless film thickness corresponding to the appearance of contact (three times the r.m.s roughness height), is approximately equal to 0.5. Above this value, the present model is correct. Below this threshold mixed lubrication is expected to occur. This boundary between full film and mixed lubrication regimes has been added on the temperature map (dashed curve):
, the film thickness can reach zero at low sealing number values. In this case face contact will be experienced. According to my experience, the dimensionless film thickness corresponding to the appearance of contact (three times the r.m.s roughness height), is approximately equal to 0.5. Above this value, the present model is correct. Below this threshold mixed lubrication is expected to occur. This boundary between full film and mixed lubrication regimes has been added on the temperature map (dashed curve):
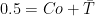
It is now necessary to consider contact between the surfaces of the seal.
References
Brunetière, N. & Apostolescu, A. A Simple Approach to the ThermoElastoHydroDynamic Behavior of Mechanical Face Seals Tribology Transactions, 2009, 52, 243-255