Seal faces lubrication
In this post, we will determine the fluid force developed between the seal faces. For that the following assumptions are used (Brunetière and Apostolescu, 2008):
- The problem is axisymetric,
- The faces are separated by an isoviscous full fluid film
- The seal faces are perfectly coned
- The seal is narrow so that its curvature can be neglected.
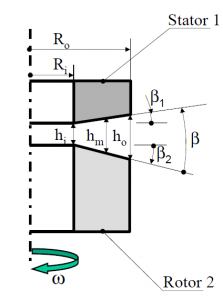
The configuration of the problem is described on the next figure.
 The pressure distribution
The pressure distribution is governed by the following Reynolds equation:
Because of the coning , the radius
and the film thickness
are linearly linked:
The Reynolds equation is now:
An analytical expression of the pressure is obtained. If the inner pressure is zero, it is:
By integrating the pressure over the seal surface , the fluid opening force
is obtained as a function of the film thickness and the outer pressure
:
This force must be balanced by the closing force due to the sealed fluid pressure and elastic elements. These forces are described on the next figure.
 The closing force can be expressed in this way:
The closing force can be expressed in this way:
is a global balance ratio including the effect of the fluid and the spring force
. If the fluid pressure is high enough, the total balance ratio is equal to seal balance ratio
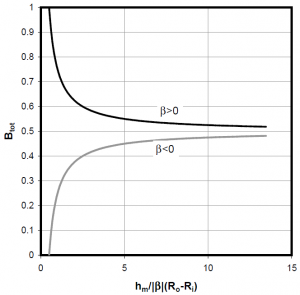
The force balance leads to an equation giving the mean film thickness $h_m$ as a function of the total balance ratio and the coning angle:
As illustrated on the next figure, a positive coning angle is necessary to obtain a stable full fluid film as demonstrated by Green and Etsion (1985). Moreover, the balance ratio must be higher than 0.5 to avoid an opening of the seal and lower than 1 to prevent from faces contact.
References
Brunetière, N. & Apostolescu, A. A Simple Approach to the ThermoElastoHydroDynamic Behavior of Mechanical Face Seals Tribology Transactions, 2009, 52, 243-255
Green, I. & Etsion, I. Threshold and Steady-State Response of Noncontacting Coned-Face Seals ASLE Transactions, 1985, 28, 449-460