Tag Archives: simulation

Online simulation of mechanical seals is now possible

Posté le 24 January 2020 by Noël Brunetière - 1,720 views vues

As explained in the previous posts (link), the behavior of mechanical seals is governed by several physical phenomena in interaction: lubrication, asperity contact, heat transfer, deformation. It makes the analytical calculation of mechanical seals complicated.

The software SimMS (Simulation of Mechanical Seal) that I developed at Institut Pprime is now available online (SimMS Online) thanks to Uniwaresity. It is a useful tool to compute the behavior of mechanical seal.

> Try it

Example of simulation with SimMS (source Uniwaresity)

Analytical modelling of mechanical face seals: post #3

Posté le 4 November 2011 by Noël Brunetière - 2,324 views vues

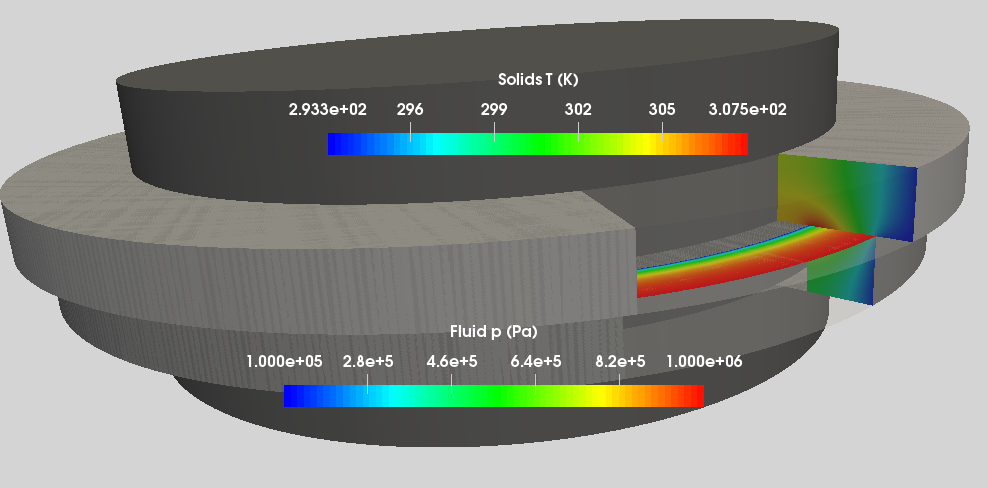
Seal faces lubrication

In this post, we will determine the fluid force developed between the seal faces. For that the following assumptions are used (Brunetière and Apostolescu, 2008):

The problem is axisymetric,
The faces are separated by an isoviscous full fluid film
The seal faces are perfectly coned
The seal is narrow so that its curvature can be neglected.

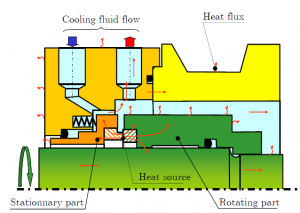
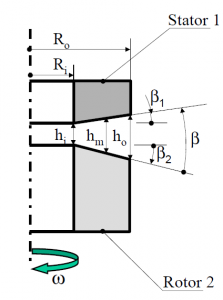
The configuration of the problem is described on the next figure.

The pressure distribution $p$ is governed by the following Reynolds equation:

$\frac{d}{dr}\left( h^3 \frac{dp}{dr}\right) =0$

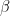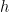Because of the coning $\beta$ , the radius $r$ and the film thickness $h$ are linearly linked:

$h=h_i+\beta \left(r-r_i \right)$

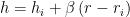
The Reynolds equation is now:

$\frac{d}{dh}\left( h^3 \frac{dp}{dh}\right)=0$

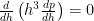
An analytical expression of the pressure is obtained. If the inner pressure is zero, it is:

$p\left( h \right)=p_o\left( \frac{h_o^2}{h^2}\frac{h^2-h_i^2}{h_o^2-h_i^2}\right)$

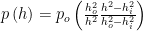
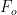By integrating the pressure over the seal surface $S_f$ , the fluid opening force $F_o$ is obtained as a function of the film thickness and the outer pressure $p_o$ :

$F_o=p_o\frac{h_o}{h_o+h_i}S_f= p_o\frac{2h_m+\beta \Delta R}{4h_m}S_f$

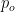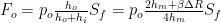
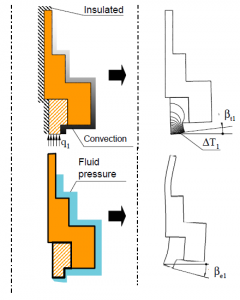
This force must be balanced by the closing force $F_c$ due to the sealed fluid pressure and elastic elements. These forces are described on the next figure.

The closing force can be expressed in this way:

$F_c=p_o\left(B+\frac{F_s}{p_o S_f} \right)S_f=p_oB_tS_f$

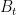$B_t$ is a global balance ratio including the effect of the fluid and the spring force $F_s$ . If the fluid pressure is high enough, the total balance ratio is equal to seal balance ratio $B=\frac{r_o^2-r_h^2}{r_o^2-r_i^2}$

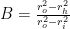
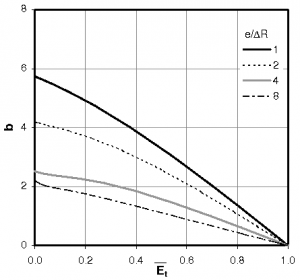
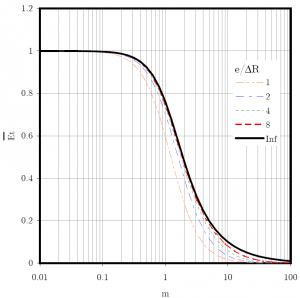
The force balance leads to an equation giving the mean film thickness $h_m$ as a function of the total balance ratio and the coning angle:

$h_m=\frac{\beta \Delta R}{4 \left(B_t-0.5 \right)}$

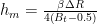
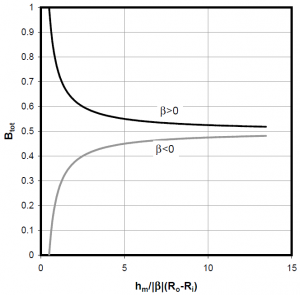
As illustrated on the next figure, a positive coning angle is necessary to obtain a stable full fluid film as demonstrated by Green and Etsion (1985). Moreover, the balance ratio must be higher than 0.5 to avoid an opening of the seal and lower than 1 to prevent from faces contact.

References

Brunetière, N. & Apostolescu, A. A Simple Approach to the ThermoElastoHydroDynamic Behavior of Mechanical Face Seals Tribology Transactions, 2009, 52, 243-255

Green, I. & Etsion, I. Threshold and Steady-State Response of Noncontacting Coned-Face Seals ASLE Transactions, 1985, 28, 449-460

Analytical modelling of mechanical face seals: post #2

Posté le 11 October 2011 by Noël Brunetière - 2,117 views vues

Deformation of the seal faces

The second step of the model concerns deformation of the mechanical seal faces. To be able to accurately determine the behavior of the seal it is mandatory to know the geometrical configuration of the seal faces. Usually, the magnitude of the deformations is a couple of microns (Doust and Parmar, 1986) to be compared to the distance between the faces which is of the order of a micron. The model presented here is axisymetric and thus the deformation considered is an angular deformation leading to a conical shape of the faces. It can be measured by mean of a taper or coning angle as illustrated on the next figure.

Two types of deformation can be identified (Doust and Parmar 1986). The first one is due to thermal gradient in the rings and leads to a coning angle $\beta_t$ . This angle is proportional to the seal face temperature rise $\Delta T$ leading to the following rotation:

$\beta_t=N \Delta T$

where $N$ is the thermal rotation rate. It is important to note that for many seal rings design, the coefficient $N$ is positive if calculated as indicated on the previous figure.

An additional deformation $\beta_e$ is due to the mechanical loading generated by the sealed fluid pressure and the springs, O-rings, etc. Unfortunately, there exists no analytical solution of this problem and these angles must be calculated by FEA. However, these coefficients remain constant as long as the boundary conditions are unchanged. For example, the next figure presents the evolution of $b=N/\lambda$ as a function of $\bar{E_t}$ for a rectangular ring of length $e$ , width $\Delta r$ and radii ratio of 0.88. Here $\lambda$ is the thermal expansion coefficient of the material.

The total coning angle $\beta$ can be expressed in this way:

$\beta=N \Delta T+\beta_e$

Reference

Doust, T. & Parmar, A. An Experimental and Theoretical Study of pressure and thermal Distortions in a Mechanical Seal ASLE Transactions, 1986, 29, 151-159

Analytical modelling of mechanical face seals: post #1

Posté le 4 July 2011 by Noël Brunetière - 2,321 views vues

Heat transfer in mechanical seals

The first step of the model concerns heat transfer in the mechanical seal rings. As illustrated in the following figure, the mechanism of heat transfer in the vicinity of mechanical seal could be quite complicated.

However it has been shown that the heat generated in the seal interface is mainly transferred by conduction through the rings to the surrounding sealed fluid and then removed by convection. The heat transfer or convection coefficient is $h_c$ . This parameter in mechanical seal can be evaluated using the Becker’s correlation (Becker 1963).

The previous figure shows the temperature distribution in the stationary part (part 1) of the seal when submitted to a heat flux $q_1$ . The average resulting temperature rise of the face is $\Delta T_1$ . Let us introduce the thermal efficiency $E_{t1}$ of the ring 1 defined as the ratio of the thermal power $P_1$ entering the face to the average temperature rise.

$E_{t1} = \frac{P_1}{\Delta T_1}= \pi \left( r_o^2-r_i^2\right)\frac{q_1}{\Delta T_1}$

where $r_o$ and $r_i$ are respectively the outer and inner radii of the seal interface.

For a given seal design, this coefficient is only dependent on the thermal boundary conditions and can easily be calculated with a FEA software. If the seal width $\Delta r=r_o- r_i$ is very small compared to the ring length $e$ , an analytical expression of $E_{t}$ can be found using the fin theory (Buck, 1989):

$E_t = 2 \pi r_oe h_c \frac{\tanh m}{m}$

where $m$ is a heat transfer parameter including $h_c$ and the thermal conductivity of the ring $k$ :

$m = \frac{e}{\Delta r} \sqrt{ \frac{h_c \Delta r }{k} }$

A dimensionless version of the thermal efficiency can be expressed in this way:

$\bar{E_t}=\frac{E_t}{2 \pi r_oeh_c }$

The evolution of the dimensionless thermal efficiency is presented on the next figure as a function of the thermal parameter $m$ (black solid curve). On the same figure, results obtained with FEA are presented when the seal ring length is varied from 1 to 8 and for a radii ratio of 0.88. It can be seen that the analytical solution is a reasonable approximation when the seal length is more than 4 times the seal width.

If the two seal rings are supposed to be at the same temperature $\Delta T= \Delta T_1= \Delta T_2$ , a global thermal efficiency $E_t$ , being the sum of the two individual thermal efficiencies, can be defined. The total thermal power $P$ entering the seal faces is thus:

$P=E_t \Delta T= \left(E_{t1}+ E_{t2}\right)\Delta T$

References

Becker, K. “Measurement of Convective Heat Transfer from a Horizontal Cylinder Rotating in a Tank of Water,” International Journal of Heat and mass Transfer (6), 1963, pp. 1053-1062.

Buck, G. “Heat Transfer in Mechanical Seals”‘Proceedings of the 6th International Pump Users Symposium’, Houston, Texas, USA, 1989, pp. 9-15.